缠论K线分为独立K线和包含关系。
前文咱们说过了K线的序列,有序列的K线就是独立K线。K线的序列分为上涨序列和下跌序列,具体请移步第一课去看。
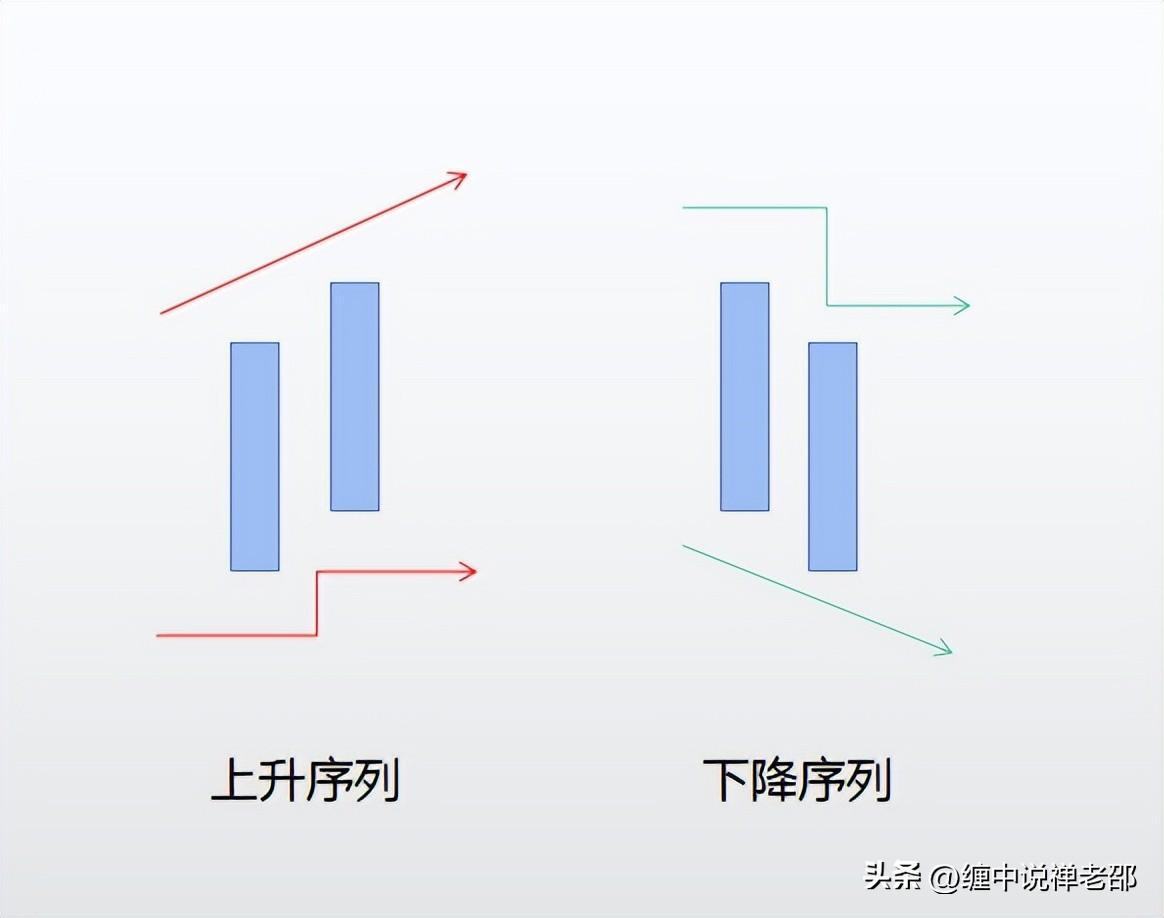
今天要解决的,就是两根K线的序列不明确的关系。
做人,就是要清清楚楚,明明白白,不要拉拉扯扯,不明不白。
不明确的关系,基本上就是以下六种,统称为包含关系。
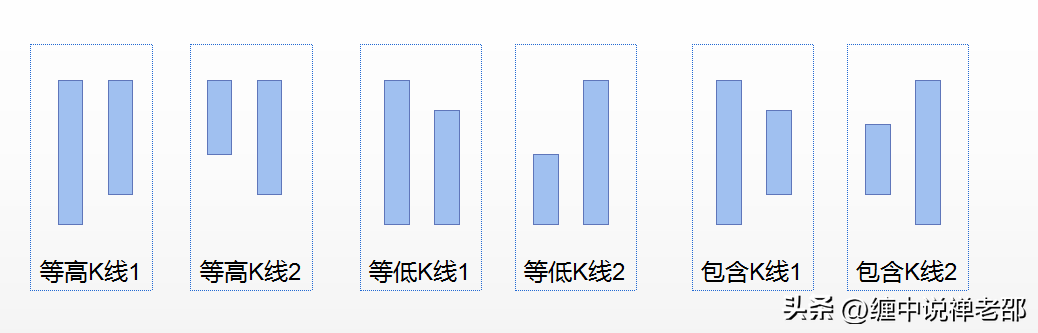
K线处理算是缠论中的第一个难点。也是很多人学习缠论,中途放弃的原因。道德经云,民之从事,常于几成而败之。慎终如始,则无败事。学会K线处理,既是学习缠论的第一步,也是迈向成功的最关键一步。
K线处理的原则, 是遵循序列的顺序。
具体方法就是以合并前的K线序列为准。如果前面的K线也没有序列,则继续往前推,以前面的序列为准。
举例如下。
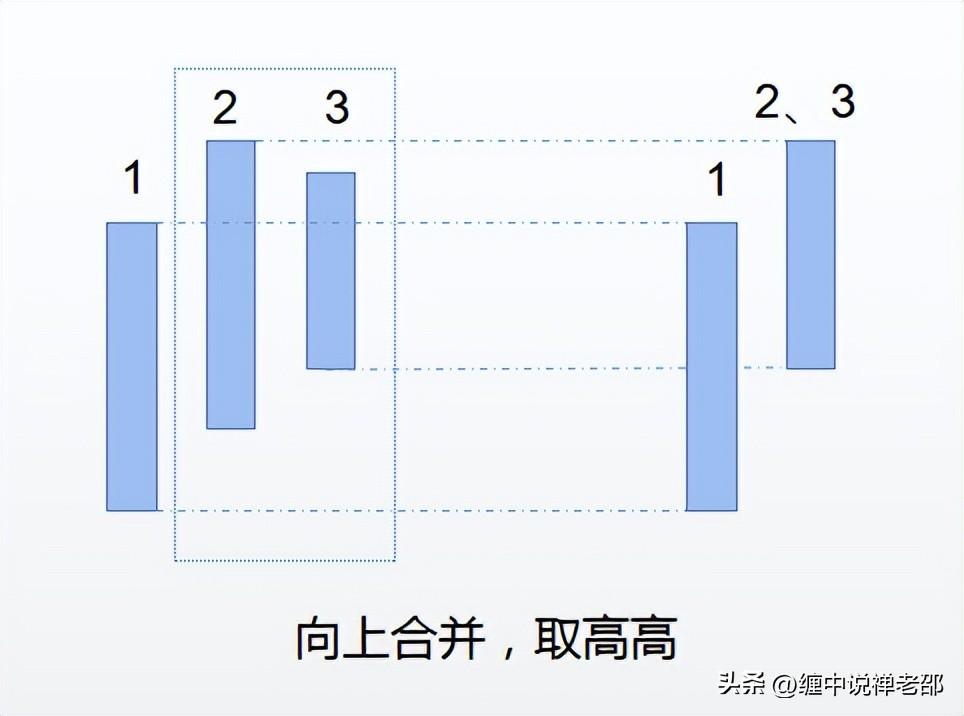
如上图所示,【2,3】K线有包含关系,要进行合并处理。此时做的第一个动作就是往前看2和1的K线是否有序列,如果有,按照1,2的K线序列处理。图中【1,2】K线的序列是向上,的,则【2,3】K线的序列就是向上取合并。向上取合并的口诀是取高高,就是取2的高点和3的高点中较高的那一个作为新K线的高点,取2的低点和3的低点中较高的那一个作为新K线的低点,则得到新的K线就是【2的高点】和【3的低点】组合成的新K线。1号K线则保持不变。看图更加清楚。
再来个难一点的。
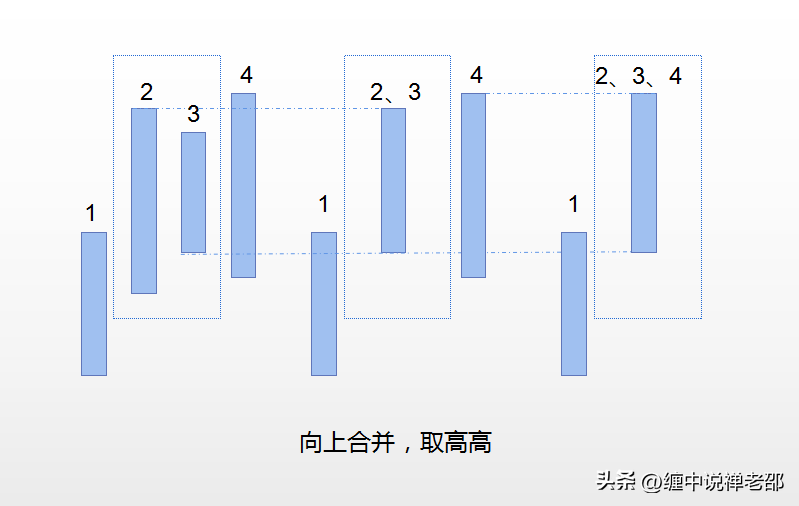
如上图所示,【3,4】K线有包含关系,要进行合并处理。此时做的第一个动作就是往前看3和2的K线是否有序列,如果有,按照1,2的K线序列处理。很可惜没有。【2,3】K线也有包含关系,现在就要再往前看1和2的K线是否有序列。如果有,就按照1,2的K线序列处理。图中【1,2】K线的序列是向上的,合并K线的顺序就是先合并【2,3】,合并之后的K线和4还是有包含关系,在合并新的【2、3,4】K线。合并的结果如上图所示。
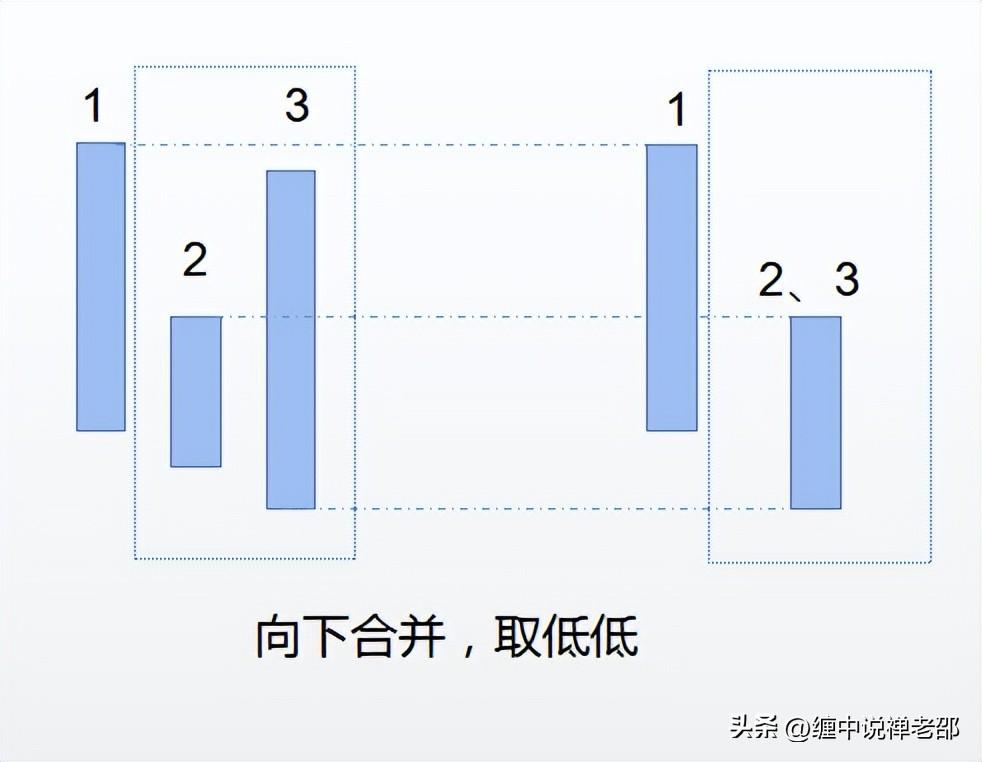
说完了向上合并,再来说一个向下合并。向下合并的口诀是取低低。
如上图所示,【2,3】K线有包含关系,要进行合并处理。此时做的第一个动作就是往前看2和1的K线是否有序列,如果有,按照1,2的K线序列处理。图中【1,2】K线的序列是向下的,则【2,3】K线的序列就是向下取合并。向下取合并的口诀是取低低,就是取2的高点和3的高点中较低的那一个作为新K线的高点,取2的低点和3的低点中较低的那一个作为新K线的低点,则得到新的K线就是【2的高点】和【3的低点】组合成的新K线。1号K线则保持不变。具体看上图。
再来个难一点的。
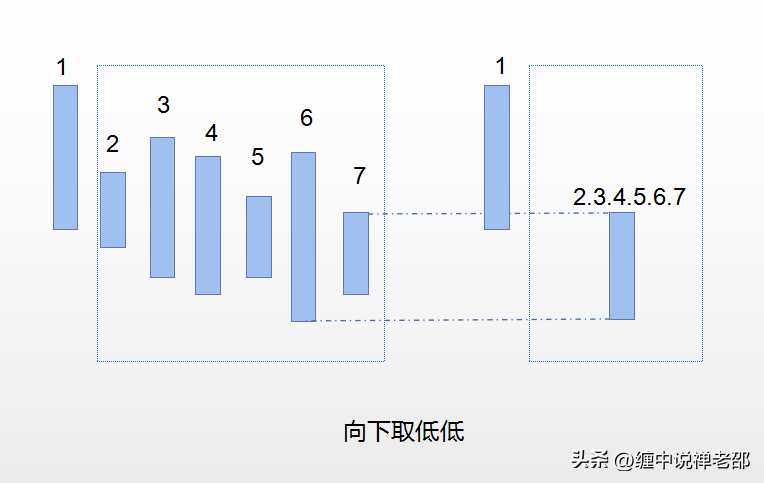
如上图,【2,3,4,5,6,7】合并成一根新的K线。
K线合并基础打扎实了,后面才有笔段中枢的演化。下篇文章,再讲笔的划分和不同的K线分类方式。